Cet article est une réédition d’une page publiée sur ce blog le 3 mai 2013, et antérieurement sur OverBlog par Gramgroum.
FightClub
AVANT-PROPOS : Qu’est-ce qu’un système de notation ?
Un système de notation est un ensemble de conventions (convention = chose dont on convient arbitrairement, sur laquelle on se met d’accord) qui permet de décrire, à l’aide de signes (généralement alphanumériques) les mouvements qu’effectuent les pièces d’un jeu abstrait sur le tablier de jeu.
Ce type de notation est appelé « notation algébrique ». D’un point de vue pratique, c’est un véritable langage international qui permet par exemple d’échanger facilement de nombreuses parties avec un simple fichier texte. Et bien avant l’ère des nouvelles technologies de communication, les systèmes de notation permettaient de diffuser des parties ou de jouer à distance, par simple courrier postal (ainsi au jeu d’échecs, où la notation existe depuis le milieu du XVIIIème siècle).
Pour dire les choses plus simplement, un système de notation est un code fait de chiffres et de lettres qui permet de décrire les coups joués.
Tout le monde a déjà joué à la bataille navale, qui est fondée sur un système de notation orthogonale (lignes se coupant en angle droit) : chaque coup joué est décrit à l’aide de deux coordonnées (une lettre et un chiffre) qui indiquent la position d’une case. C’est un système de notation très simple, dans la mesure où il n’y a pas de mouvement effectué : chaque coup joué porte le nom d’une case (par exemple : A7, C4, D8 etc.).
La notation se complique un peu quand il s’agit de décrire un déplacement. Aux échecs par exemple, la notation reste relativement simple : pour chaque coup, on indique la case de départ et la case d’arrivée d’une pièce ; aucune ambiguïté n’est possible. Ainsi, un coup noté e2-e4 signifie que la pièce qui se trouvait sur la case e2 a été déplacée sur la case e4 (Je parle de la notation des échecs complète, je n’entre pas dans les détails de la notation simplifiée, ce n’est pas l’objet ici.).
Cela se complique encore quand il s’agit de décrire les déplacements au jeu d’abalone, pour plusieurs raisons :
– les cases sont traversées par trois axes, on n’a donc pas d’orthogonalité (ce qui est déroutant, mais n’est pas gênant en soi ; nous verrons plus loin que les systèmes de notation ont en fait « réintégré » l’orthogonalité),
– le joueur peut déplacer une, deux ou trois pièces de même couleur en un même coup,
– le joueur peut pousser une ou deux billes adverses (ce n’est pas indifférent, nous le verrons lorsque nous aborderons la question de la réversibilité).
LA NOTATION DU JEU D’ABALONE
Très tôt dans l’histoire d’abalone, différents systèmes de notations ont été mis en oeuvre. Certains ont disparu, en raison de leurs défauts (ambiguïté, lourdeur…). D’autres ont subsisté et cohabitent aujourd’hui. Parmi ceux-ci, deux systèmes assez proches l’un de l’autre se sont imposés et sont généralement utilisés : les systèmes Aba-Pro et Nacre (Aba-Pro et Nacre furent longtemps les deux plus fortes intelligences artificielles d’abalone ; voir l’article Des intelligences artificielles : les programmes existants). Notons que MiGs et MLA n’ont pas de système de notation qui leur soit propre, et laissent le choix entre ces deux systèmes.
Avant d’en venir à ces deux systèmes, disons quelques mots sur les autres tentatives, où Aba-Pro et Nacre plongent parfois leurs racines.
1) Les tentatives de Marc Ghigou
En 1989, la défunte Fédération Française d’Abalone proposait un système de notation dû à Marc Ghigou, fondé sur la notation du plateau suivante :
Il s’agit d’un article paru dans le magazine Jeux & Stratégies du mois de novembre 1989, qui explique ce système. Celui-ci était si compliqué et source de tant d’ambiguïtés qu’il n’a jamais été vraiment utilisé.
Dès le mois de mai 1990, la Fédération a adopté un nouveau système de notation, qui se présentait ainsi :
Il s’agit d’un article paru dans Jeux & Stratégies du mois de mai 1990, qui vous explique ce système (c’était, je crois, l’avant-dernier numéro de ce magazine avant sa disparition).
Plus pratique que le précédent, ce système présente néanmoins des inconvénients, notamment en ce qui concerne la notation des cases : si les lignes horizontales sont désignées par une lettre, les lignes transversales en revanche ne sont pas nommées, et chaque case se voit attribuer un chiffre dépendant de sa position sur la ligne horizontale ; de sorte que deux cases traversées par la même ligne transversale ne sont pas nécessairement désignées par le même chiffre (ainsi E2 et F1 sont sur la même ligne transversale). Remarquez la conclusion un peu prophétique de l’article.
2) Les travaux de Michael Frank
A peu près à la même époque, c’est-à-dire au début des années 1990, de l’autre côté de l’Atlantique, on réfléchissait à la programmation d’abalone et par la même occasion aux systèmes de notation. Vous trouverez ici des échanges entre Michael Frank, du MIT (Massachusetts Institute of Technology), et d’autres chercheurs sur ce sujet.
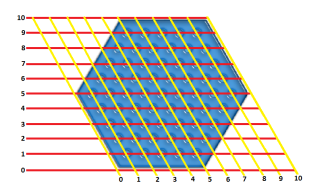
Michael Frank s’est aperçu qu’il pouvait placer les cases du plateau d’abalone dans un système orthogonal, chaque case étant ainsi désignée selon l’abscisse (axe des x) et l’ordonnée (axe des y). Il n’est pas du tout nécessaire de faire intervenir le troisième axe qui traverse chaque case. Le schéma suivant, de Michael Frank, nous montre comment l’hexagone s’inscrit dans un carré :
Plus joliment, cela nous donne :
Voilà qui était très arrangeant, au moins autant pour la construction de programmes informatiques que pour la notation elle-même. Il ne restait plus ensuite qu’à remplacer les chiffres en ordonnée par des lettres, pour éviter toute confusion. De fait, Michael Frank jetait là les bases des principaux systèmes de notations d’abalone existant encore aujourd’hui.
En ce qui concerne la notation des déplacements, je vous laisse suivre vous-mêmes les tâtonnements de Michael Frank (ici). Sachez qu’il n’est pas parvenu à une notation vraiment aboutie. Je relève au passage l’idée de départ assez intuitive de désigner les directions à l’aide des points cardinaux, idée qui sera toutefois abandonnée.
3) Autres systèmes de notation
D’autres systèmes ont existé (ou existent encore de manière marginale). J’en citerai deux qui n’utilisent pas de coordonnées pour nommer les cases, mais un simple système de numérotation.
– le système LMU (Loyola Marymount University – Los Angeles, 1994) qui numérote les cases de 0 à 60. J’ignore comment sont notés les déplacements dans ce système.
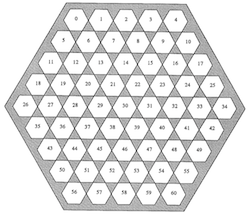
– le système OKUN, que vous pouvez découvrir en cliquant sur l’image ci-dessous, qui numérote les cases de 1 à 61.
(à suivre : les notations Nacre et Aba-Pro)
Gramgroum